ディゾルバー高速撹拌機は、円盤の円周上に上下交互に折り曲げられた羽根のある形状をしています。容器に対して比較的小型の翼を配置し翼先端速度(周速)を10m/s~25m/s程度に回転させることで、凝集物の解砕などの分散に利用されています。


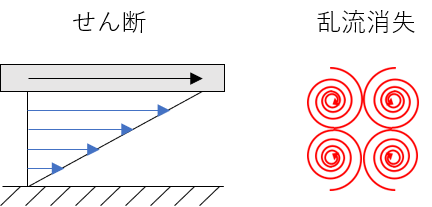
今回は、凝集物の解砕などの分散が流体の変形により生じると考え、周速の速い翼先端付近で生じる次の図のような「せん断」と「乱流消失」を計算しました。
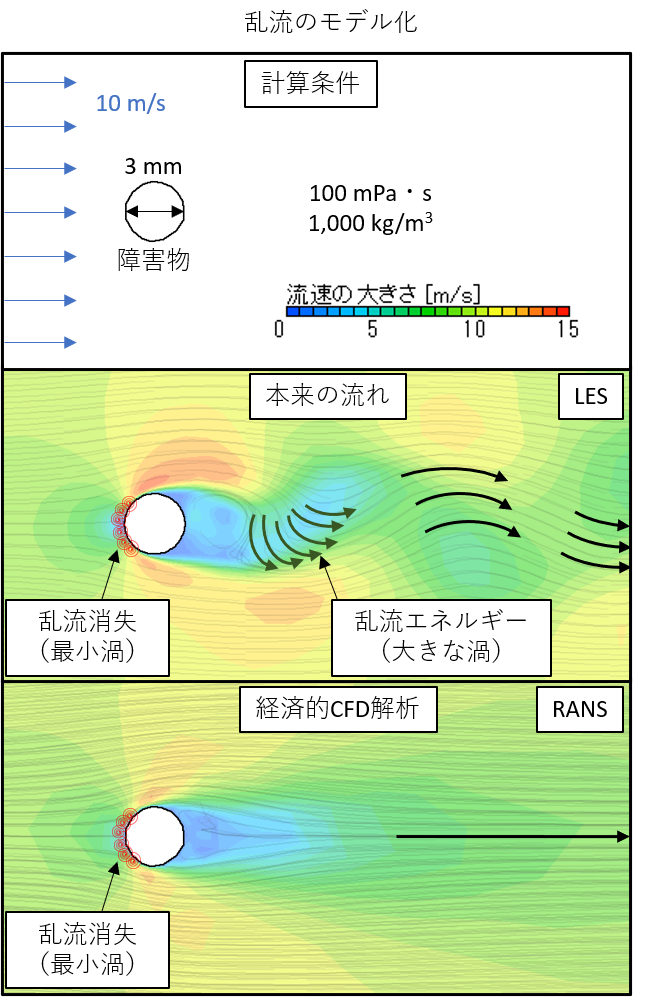
ただし、経済的なCFD解析のために主に2つのモデル化という制約があります。一つは次の図の乱流のモデル化です。3 mmの障害物がある空間に100 mPa・s、1,000 kg/m3の流体を10 m/sで流しています。本来の流れであれば、障害物の前方に最小渦である乱流消失が生じ、障害物の後方に大きな渦である乱流エネルギーが生じ流れが蛇行します。一方、経済的CFD解析では障害物前方の乱流消失は生じますが、障害物後方の乱流エネルギーはほとんど再現できず、流れが蛇行していません。経済的なCFD解析では障害物の後方の流れの詳細は再現できません。
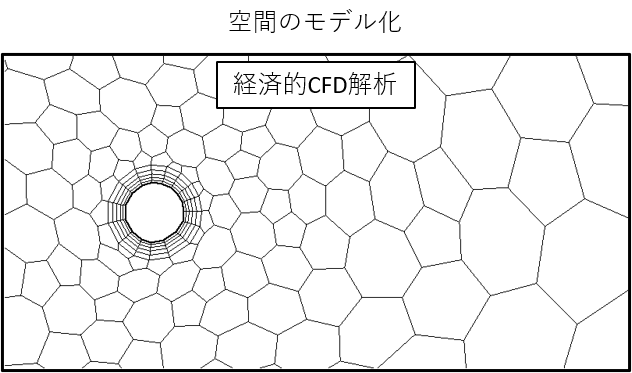
二つ目のモデル化は次の図の空間のモデル化です。本来の空間の最小分解能は分子サイズであると考えられますが、経済的CFDではこの分解能について、ある程度妥協する必要があります。前述の3 mmの障害物がある空間における空間分解能は、次の図のように1 mm程度で4角形や5、6角形などの重心で計算をします。分解能の結果については後程解説しています。
ミキサー条件として、次の条件でCFD解析を行いました。ディゾルバー高速撹拌機による撹拌のCFD解析混合編と同じ条件です。
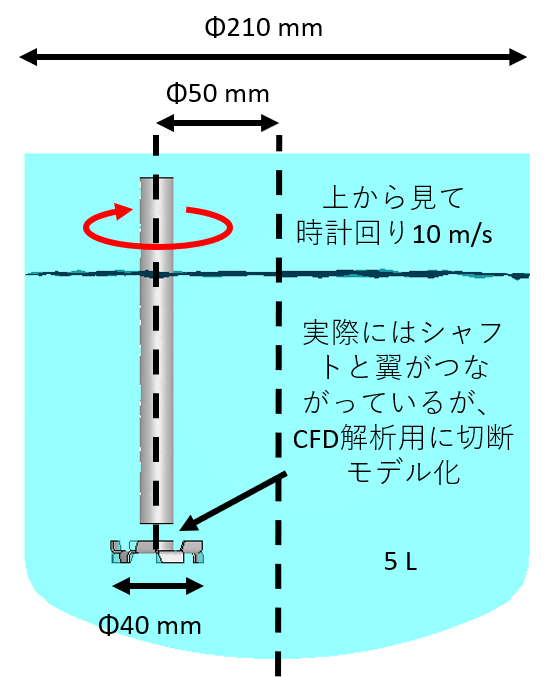
| 翼先端周速 | 10 m/s |
| 処理液 | 5 L |
| 粘度 | 100 mPa・s |
| 密度 | 1000 kg/m3 |
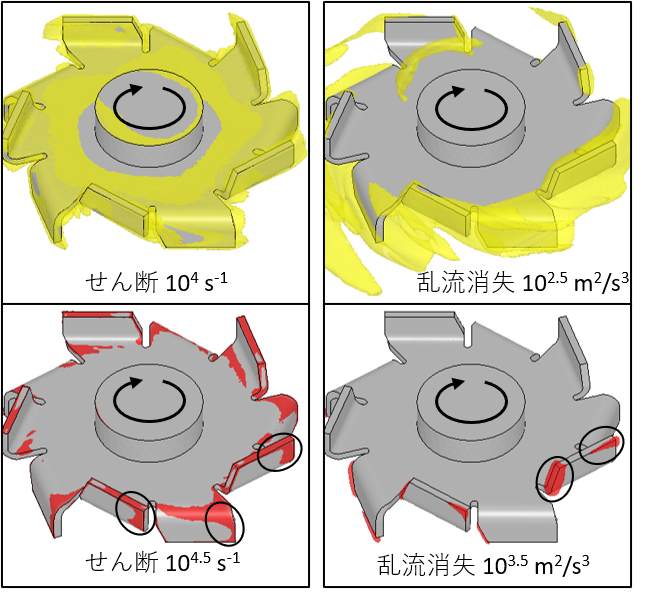
始めに定性分析として、「せん断」と「乱流消失」の分布について次に示します。左上のせん断104s-1は翼の表面のほぼ全面と翼の後方に分布しており、左下の高いせん断の104.5s-1は翼先端の後方の表面にあります。せん断は翼と流体の速度差の大きい部分に生じると考えられます。一方、右上の乱流消失102.5 m2/s3は翼の先端の表面から少し離れて分布しており、右下の高い乱流消失103.5 m2/s3は翼先端の後方と前方に表面から盛り上がってあります。乱流消失は翼と流体が衝突する部分で生じると考えられます。このせん断と乱流消失が凝集物の解砕などの分散にどのように作用するのかについては、まだ詳細がわかっておりませんが、速度差や衝突が寄与していると思われます。
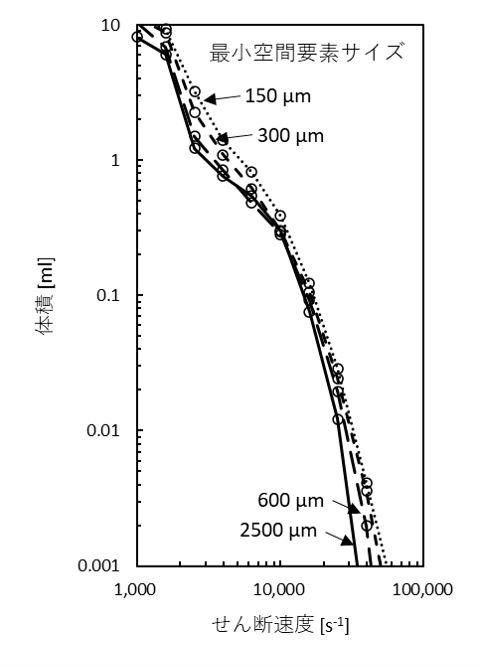
次に定量分析として、「せん断」の値における体積分布を次に示します。横軸にせん断速度、縦軸にその体積を表示し、図中の最小空間要素サイズは、空間のモデル化において設定した最小要素サイズです。いずれの最小要素サイズにおいても、せん断速度が高くなるに従い、その体積が減少しておりますが、その体積の量に差があり最小空間要素サイズが小さいほど、その体積が多くなりました。
次に定量分析として、「乱流消失」の値における体積分布を次に示します。横軸に乱流消失率、縦軸にその体積を表示しています。せん断の体積分布と同様にいずれの最小要素サイズにおいても、乱流消失率が高くなるに従い、その体積が減少しておりますが、その体積の量に大きな差があり最小空間要素サイズが小さいほど、その体積が多くなりました。
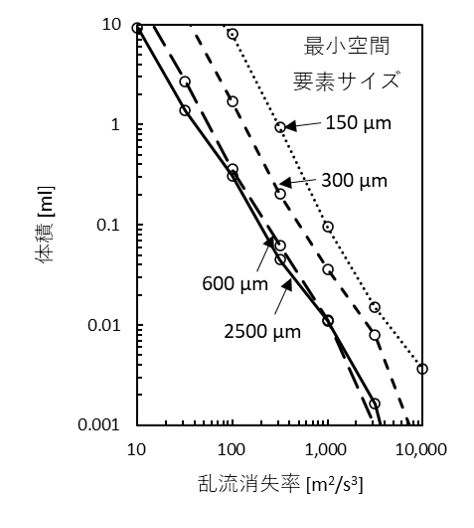
「せん断」と「乱流消失」の定量分析から、最小空間要素サイズが変わった場合、異なる結果となってしまうことがわかります。最小空間要素サイズが小さいほど、その体積が多くなることから、最小要素サイズが大きすぎるため、本来は狭い範囲で高い数値であるはずの結果が、大きい要素サイズにより平均化されていると考えられます。経済的CFDではこの要素サイズについて、ある程度妥協する必要があるため、正確な結果を得るのが困難なのが現状です。
今回はディゾルバー高速撹拌機による分散をテーマにCFD解析しました。凝集物の解砕などの分散が翼先端で生じることが、イメージできたと思います。「せん断」や「乱流消失」などの狭い空間における分析は、主に2つのモデル化により定量分析が困難であるものの、どの部位が寄与していそうかという定性分析や、解析メッシュ作成方法を合わせたモデル同士を比較分析することは可能です。CFD解析はコンピュータによる架空のシミュレーションであることから、なんらかの妥当性検証が不可欠です。今回の例では分散処理液の粒度分布測定などにより検証が可能です。
